상세 컨텐츠
본문
맨 하단에 링크를 걸어둔 이 사이트에서는 simulated annealing 일명 담금질 알고리즘으로 외판원 문제(TSP)를 푸는 툴을 제공한다.
외판원 문제(TSP : Traveling Salesman Problem)란 여러 도시를 모두 방문해야 하는 세일즈맨의 최단 거리 최적 경로를 찾는 문제이다.
외판원 문제의 해는 항상 단일 폐곡선(simple closed curve)으로 나오게 된다.
하지만 지나야 하는 점의 수가 늘어날수록 경우의 수가 워낙 많아지기 때문에 모든 경우의 수를 다 따지기는 쉽지 않다.
컴퓨터를 이용하여 많은 경우의 수를 시행해보며 좋은 결과를 찾아나간다.
이러한 여러 경우의 수를 시행해보면서 해를 찾는 기법을 통틀어서 heuristic algorithm이라고 한다.
그 중에서 simulated annealing은 초기에는 넓은 탐색을 하다가 점차 탐색 범위를 좁히는 방식이다.
heuristic algorithm은 이외에도 유전 알고리즘이나 Greedy 알고리즘 등이 있다.
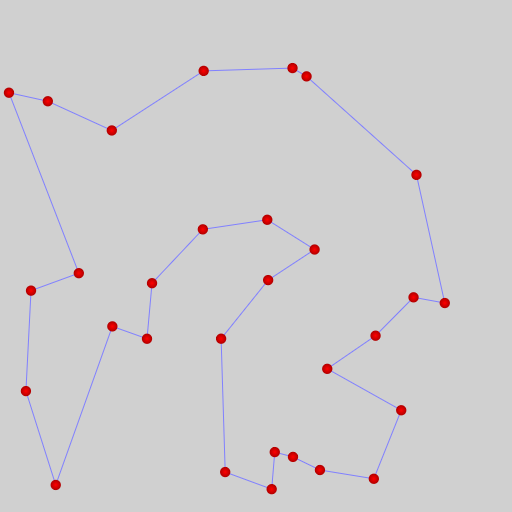

두 가지 경우를 비교해보자. 둘 다 단일 폐곡선을 이루면서 해를 제시했다. 결론적으로 보면 아래보다는 위의 결과가 더 좋게 나왔다. 차이는 0.5%정도. 위의 방법이 아래의 방법보다 더 좋다는 것을 직접 모두 계산하는 것 외에 입증하기는 쉽지 않다. (현재로서는 수학적으로 발견되지 않았다.) 만일 가능한 방법이 있다고 하더라도 직접 계산해서 비교하는 것보다 효율적일지는 따져봐야 한다.
수학적으로 깊이있게 P-NP 문제 라고하는데 너무 말이 길어지니까 이 얘기는 접어두겠다.
아무튼 이 TPS 문제는 수학적으로 NP-완전 문제에 속하며 계산을 다 해서 검산하는 것보다 더 좋은 계산 방법이 아직 발견되지 않았다. 그렇다고 더 좋은 계산 방법이 없다고 증명되지도 않았다. 아무튼 복잡한 이야기이다.
https://www.fourmilab.ch/documents/travelling/anneal/
Simulated Annealing: The Travelling Salesman Problem
Given a list of cities and their locations (usually specified as Cartesian co-ordinates on a plane), what is the shortest itinerary which will visit every city exactly once and return to the point of origin? Easy to ask, but devilishly difficult to answer
www.fourmilab.ch
'주저리 주저리 > 내 생각' 카테고리의 다른 글
| 알씨 대신 이걸 써보자 (1) | 2025.04.23 |
|---|---|
| 도널드 트럼프가 2024년 미국 대선에서 승리한 결정적 이유 (0) | 2024.11.21 |
| 11번가 등급제 종료 (1) | 2023.04.05 |
| 네이트온 업데이트시 주의사항 (0) | 2022.09.28 |
| 포레스텔라 팀 이름의 유래(추측글) (0) | 2022.09.05 |






댓글 영역